 |
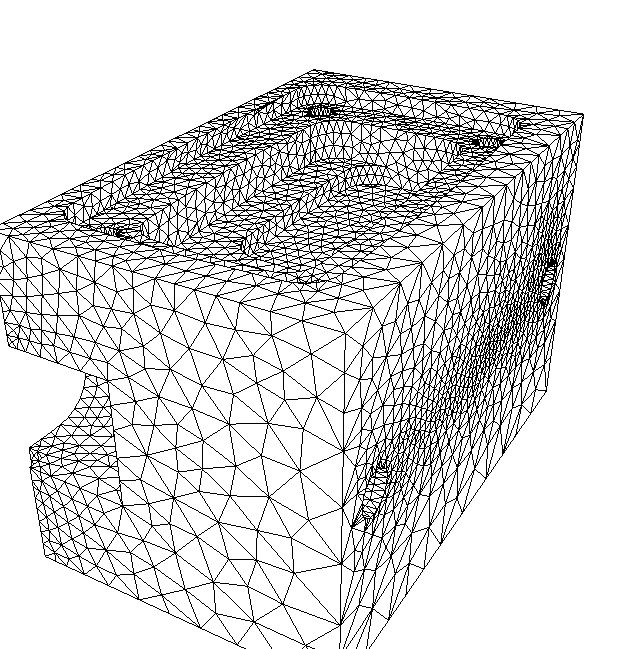
| A finite-element 3D triangular mesh example of a part (image adapted from here). |
To solve for the displacement or deformation due to an applied load on our solid object, we formulate our problem as a system of equations in terms of matrices, where each matrix represents one element. In our example problem, we make the assumption that the entire structure is in equilibrium and thus each element must also be in equilibrium. To find the displacement at each node we use Hooke's law for elastic response:
$$ \mathbf{\sigma} = \mathbf{E}\cdot\mathbf{\epsilon}$$
where $\mathbf{\sigma}$ is the stress, $E$ Young's modulus, and $\epsilon$ the strain. The strain is given by the following displacement node matrix,
\[\mathbf{\epsilon}=\begin{bmatrix}\frac{\partial}{\partial x} & 0 \\ 0 & \frac{\partial}{\partial y} \\ \frac{\partial}{\partial y} & \frac{\partial}{\partial x} \end{bmatrix}\mathbf{u}\]
here $\mathbf{u}$ is the node displacement. In matrix notation, Hooke's law reads,
\[\mathbf{\sigma} = \frac{E}{\left(1+\nu\right)\left(1+2\nu\right)}\begin{bmatrix}1-\nu & & \\ \nu & 1-\nu & \\ & & \frac{\left(1-2\nu\right)}{2}\end{bmatrix}\mathbf{\epsilon}\]
As mentioned the solid body is in mechanical equilibrium and so the work being done by external loads balances with the work done by internal forces. The equilibrium of node $i$ acted on by force, $F_i$, is written as:
$$\delta \mathbf{u}_{i}^T\mathbf{F}_i = \int_{V} \delta \mathbf{\epsilon}^{T}\mathbf{\sigma}dV$$
The integrand can then be expressed in terms of the element stiffness matrix, $\mathbf{K}$, and displacements at node $i$ can be solved for the applied load. The operations would be:
where $\mathbf{P}_i$ is the applied load at each node. The majority of the effort in FEM is the inversion of the stiffness matrix. Due to the complexity of the mesh and geometry, numerical methods are typically used to solve FEM problems.
I hope this was a useful refresher to FEM, if you have any suggestions feel free to add them in the comment section. Finding a quote for this post was no easy task but I found this one which I slightly modified:
"The innards of Ping's G5 golf club were supposedly computer-engineered with a process called finite-element analysis, a term that for all I know was stolen from a Star Trek episode."
-Carl Hiaasen, The Downhill Lie: A Hacker's Return to a Ruinous Sport
here $\mathbf{u}$ is the node displacement. In matrix notation, Hooke's law reads,
\[\mathbf{\sigma} = \frac{E}{\left(1+\nu\right)\left(1+2\nu\right)}\begin{bmatrix}1-\nu & & \\ \nu & 1-\nu & \\ & & \frac{\left(1-2\nu\right)}{2}\end{bmatrix}\mathbf{\epsilon}\]
As mentioned the solid body is in mechanical equilibrium and so the work being done by external loads balances with the work done by internal forces. The equilibrium of node $i$ acted on by force, $F_i$, is written as:
$$\delta \mathbf{u}_{i}^T\mathbf{F}_i = \int_{V} \delta \mathbf{\epsilon}^{T}\mathbf{\sigma}dV$$
The integrand can then be expressed in terms of the element stiffness matrix, $\mathbf{K}$, and displacements at node $i$ can be solved for the applied load. The operations would be:
- Assemble the stiffness matrix $\mathbf{K}$
- Apply boundary conditions
- Calculate the displacements at each node $i$ by solving the equation:
where $\mathbf{P}_i$ is the applied load at each node. The majority of the effort in FEM is the inversion of the stiffness matrix. Due to the complexity of the mesh and geometry, numerical methods are typically used to solve FEM problems.
I hope this was a useful refresher to FEM, if you have any suggestions feel free to add them in the comment section. Finding a quote for this post was no easy task but I found this one which I slightly modified:
"The innards of Ping's G5 golf club were supposedly computer-engineered with a process called finite-element analysis, a term that for all I know was stolen from a Star Trek episode."
-Carl Hiaasen, The Downhill Lie: A Hacker's Return to a Ruinous Sport
References & Additional Reading
Reuse and Attribution
No comments:
Post a Comment
Please refrain from using ad hominem attacks, profanity, slander, or any similar sentiment in your comments. Let's keep the discussion respectful and constructive.